I am a research associate and learning technologist at Goldsmiths, University of London and working in partnership with University of London and Coursera to develop game-based learning activities. These tools are aimed at students and learners with the attempt of offering interactive and playful ways to study and understand a variety of Computer Science topics.
© 2020 Goldsmiths, University of London
All rights reserved. No part of this publication may be reproduced, distributed, or transmitted in any form or by any means without the prior written permission of the publisher, except in the case of brief quotations embodied in critical reviews and certain other noncommercial uses permitted by copyright law.
Game Type
The “Dijkstra’s Algorithm” interactive learning environment is a Puzzle, Point & Click game which attempts to abstract the complexity of the Dijkstra’s Algorithm and acts as a practice space.
This is a learning based game but should be integrated with additional resources previous to exploring it.
Description
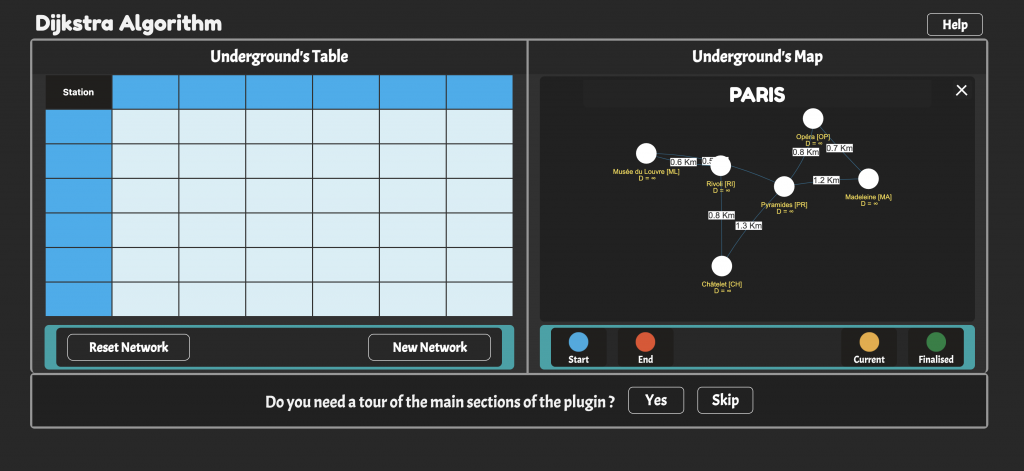
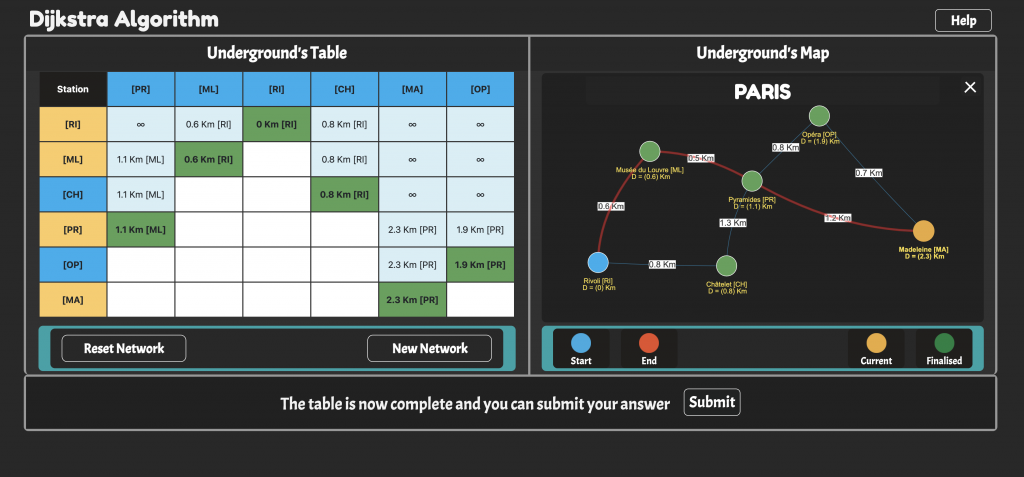
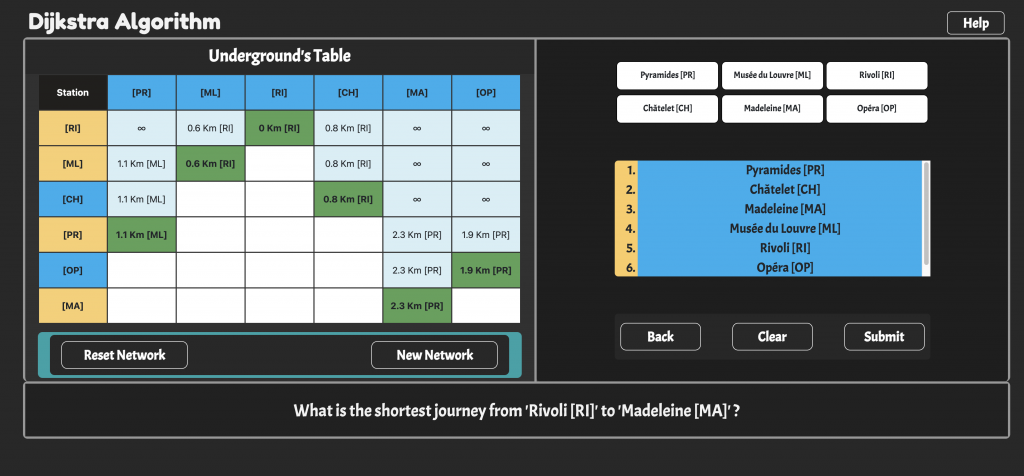
Dijkstra’s algorithm is an algorithm for finding the shortest paths between nodes in a graph. The graph may represent road networks or railroads as an example. The original algorithm finds the shortest path between two given nodes. This variant, instead, fixes a single node as the “source” node and finds shortest paths from the source to all other nodes in the graph. Nodes are connected by weighted edges. This interactive game explores the Dijkstra’s Algorithm with 5 famous underground networks around the world: Washington, London, Paris, Delhi, and Tokyo. The nodes of the graph represent stations and edge path costs represent rail distances between pairs of stations connected by a direct rail. The Dijkstra’s algorithm is used to find the shortest route between one station and all other stations in a specific underground network. Students can select their favourite underground network, choose the station they want to start their journey from, choose their destination, and correctly use the Dijkstra’s Algorithm to find the shortest journey between the stations. The interactive environment is mainly used as a practice space for students to understand and visualise the concept and steps of the algorithm. Students play in the shoes of the algorithm and need to verify the shortest path against the computer solution.
Terminal Learning Objectives
This interactive learning environment has the following TLO:
- Create a visual mental model of the Dijkstra’s Algorithm
- Understand the basics of the algorithm (nodes, edges, weight, path)
- Understand how Dijkstra can be applied to real case scenarios
Game Design Values
- Experience: The “Dijkstra’s Algorithm” interactive learning environment is a Puzzle, Point & Click game which allows the players to visualise and practice the theory of the Dijkstra algorithm.
- Theme: Players are in control of traversing underground networks and correctly executing Dijkstra’s Algorithm to find the shortest journey between stations. Underground networks are represented by graphs with nodes as stations and direct connection between nodes representing the rail routes.
- Point of View: The game is presented as a 2D environment containing images, dynamic content, and UI buttons. The game graphics are minimal but essential.
- Challenge: The main challenge is to compete against the computer in correctly traversing underground networks and by finding the shortest path between chosen stations. The networks are represented by clickable static graphs. Players have to pick their starting and ending station and successively apply the Dijkstra’s Algorithm rules to find the shortest journey. Students can visualise a table which keeps track of all the transitions made, with relative distances, and need to verify their final answer with the computer calculation.
- Decision-making: Decisions do not happen in real-time as players can take their time when making decisions.
- Skill, strategy, chance, and uncertainty: The game keeps track of players decisions and steps when traversing underground networks. Players need to combine their knowledge and correctly execute actions. There are no elements of uncertainty but players can choose different journeys within a single underground network.
- Context: The simulation is run as a web application. It has been used as part of interactive formative learning material on E-learning platforms like Coursera.
- Emotions: The “Dijkstra’s Algorithm” is meant to generate a feeling of excitement, discovery, and visual understanding. The interactive game also provides a real case scenario application of the algorithm. Students can verify their knowledge by comparing their results with the computer computation of the system.